[JAVA] 다익스트라(dijkstra) 자바로 구현하기 인접행렬, 우선순위큐
다익스트라를 자바로 구현해보자.
다익스트라의 개념에 대해서는 밑에 게시글을 참고 바란다.
[Algorithm] 다익스트라(Dijkstra) 알고리즘 자바, 파이썬
[Algorithm] 다익스트라(Dijkstra) 알고리즘 자바, 파이썬
개요 다익스트라(Dijkstra) 알고리즘은 BFS와 DP를 활용한 최단경로 탐색 알고리즘이다. 다이나믹 프로그래밍인 이유는 하나의 최단 거리를 구할 때 그 이전까지 구했던 최단 거리 정보를 그대로
gomgomkim.tistory.com
구현에는 인접 행렬 방식, 우선순위 큐 방식이 있다.
노드의 개수를 V라고 할 때 인접 행렬 방식은 O( V^2 ) 우선순위 큐 방식은 O( V log V ) 의 시간 복잡도를 가진다.
따라서 알고리즘 문제풀이 시 우선순위 큐 방식을 추천한다.
알고리즘을 이해할 때는 인접행렬 방식이 도움되었다. 순차적으로 점령하기를 추천한다.
인접행렬 방식
1. 그래프를 담을 클래스 선언 후 객체를 초기화한다.
다익스트라에서는 초기 값을 0 대신 무한대를 사용하기 때문에 => 이유는 개념편 게시글 참조
인접 행렬의 값을 int형의 MAX 값으로 초기화한다.
만약 문제에서 int 범위 이상의 값을 사용한다면, 더 큰 값으로 잡아야 한다.
class Graph{
private int n; // 노드들의 수
private int maps[][]; // 노드들간의 가중치 저장할 변수
public Graph(int n){
this.n = n;
maps = new int[n][n];
// 인접행렬 모든 값 무한대로 초기화
for(int i=0; i<n; ++i){
for(int j=0; j<n; ++j){
maps[i][j] = Integer.MAX_VALUE;
}
}
}
}
2. 인접 행렬에 가중치를 넣는 함수를 생성한다.
public void input(int i,int j,int w){
maps[i][j] = w;
maps[j][i] = w;
}
3. 다익스트라 알고리즘을 구현한다.
3-1. 최단 거리를 저장할 배열 및 노드 방문 여부 배열을 만든다.
최단 거리는 최솟값으로 업데이트할 예정이므로 초기 값은 무한대로 설정한다.
public void dijkstra(int v){
int distance[] = new int[n]; // 최단 거리를 저장할 변수
boolean[] check = new boolean[n]; // 해당 노드를 방문했는지 체크할 변수
// distance값 초기화. 무한대를 int 자료형의 최대값으로 표현했다.
for(int i=0; i<n; ++i){
distance[i] = Integer.MAX_VALUE;
}
// 시작노드값 초기화.
distance[v] = 0;
check[v] = true;
}
3-2. 인접 행렬에 초기화된 값을 이용하여 최단 거리 배열을 초기화한다.
방문하지 않았고, 초기 값이 무한대가 아닐 때 최단 거리 배열을 업데이트한다.
// 연결노드 distance갱신
for(int i=0; i<n; ++i){
if(!check[i] && maps[v][i] != Integer.MAX_VALUE){
distance[i] = maps[v][i];
}
}
3-3. 모든 노드를 돌며 최단 거리 배열 값이 가장 작은 노드를 선택해서 최소 거리를 비교한다.
비교 원리는 개념편을 참고 바란다.
for(int a=0; a<n-1; ++a){
// 원래는 모든 노드가 true될때까지 인데
// 노드가 n개 있을 때 다익스트라를 위해서 반복수는 n-1번이면 된다.
// 원하지 않으면 각각의 노드가 모두 true인지 확인하는 식으로 구현해도 된다.
int min = Integer.MAX_VALUE;
int min_index = -1;
// 노드 최소값 찾기
for(int i=0; i<n; ++i){
if(!check[i]){
if(distance[i] < min){
min = distance[i];
min_index = i;
}
}
}
// 다른 노드를 거쳐서 가는 것이 더 비용이 적은지 확인한다.
check[min_index] = true;
for(int i=0; i<n; ++i){
if(!check[i] && maps[min_index][i] != Integer.MAX_VALUE){
if(distance[min_index] + maps[min_index][i] < distance[i]){
distance[i] = distance[min_index] + maps[min_index][i];
}
}
}
}
4. 그래프 생성 및 정보 입력 후 다익스트라 알고리즘을 실행하여
한 노드로부터 모든 노드로의 최단경로를 구한다.
다익스트라 개념 게시글과 같은 예제를 사용했다.
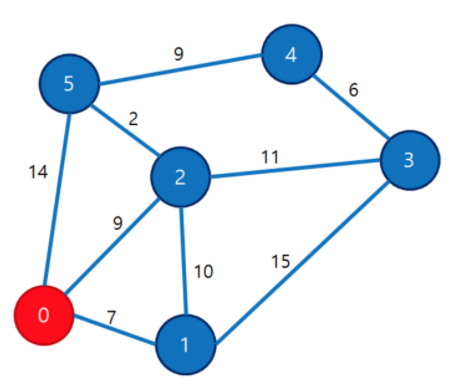
Graph g = new Graph(6); // 노드 수 만큼 그래프 생성
// 시작, 끝, 간선 가중치 입력
g.input(0, 1, 7);
g.input(0, 2, 9);
g.input(0, 5, 14);
g.input(1, 2, 10);
g.input(1, 3, 15);
g.input(2, 3, 11);
g.input(2, 5, 2);
g.input(3, 4, 6);
g.input(4, 5, 9);
// 시작노드 기준 다익스트라 알고리즘 실행
g.dijkstra(0);
전체 소스
public class Dijkstra {
public static void main(String[] args) {
Graph g = new Graph(6); // 노드 수 만큼 그래프 생성
// 시작, 끝, 간선 가중치 입력
g.input(0, 1, 7);
g.input(0, 2, 9);
g.input(0, 5, 14);
g.input(1, 2, 10);
g.input(1, 3, 15);
g.input(2, 3, 11);
g.input(2, 5, 2);
g.input(3, 4, 6);
g.input(4, 5, 9);
// 시작노드 기준 다익스트라 알고리즘 실행
g.dijkstra(0);
}
}
class Graph{
private int n; // 노드들의 수
private int maps[][]; // 노드들간의 가중치 저장할 변수
public Graph(int n){
this.n = n;
maps = new int[n][n];
// 인접행렬 모든 값 무한대로 초기화
for(int i=0; i<n; ++i){
for(int j=0; j<n; ++j){
maps[i][j] = Integer.MAX_VALUE;
}
}
}
public void input(int i,int j,int w){
maps[i][j] = w;
maps[j][i] = w;
}
public void dijkstra(int v){
int distance[] = new int[n]; // 최단 거리를 저장할 변수
boolean[] check = new boolean[n]; // 해당 노드를 방문했는지 체크할 변수
// distance값 초기화. 무한대를 int 자료형의 최대값으로 표현했다.
for(int i=0; i<n; ++i){
distance[i] = Integer.MAX_VALUE;
}
// 시작노드값 초기화.
distance[v] = 0;
check[v] = true;
// 결과값 출력
for(int i=0; i<n; ++i){
if(distance[i] == 2147483647) System.out.print("∞ ");
else System.out.print(distance[i]+" ");
}
System.out.println("");
// 연결노드 distance갱신
for(int i=0; i<n; ++i){
if(!check[i] && maps[v][i] != Integer.MAX_VALUE){
distance[i] = maps[v][i];
}
}
// 결과값 출력
for(int i=0; i<n; ++i){
if(distance[i] == 2147483647) System.out.print("∞ ");
else System.out.print(distance[i]+" ");
}
System.out.println("");
for(int a=0; a<n-1; ++a){
// 원래는 모든 노드가 true될때까지 인데
// 노드가 n개 있을 때 다익스트라를 위해서 반복수는 n-1번이면 된다.
// 원하지 않으면 각각의 노드가 모두 true인지 확인하는 식으로 구현해도 된다.
int min = Integer.MAX_VALUE;
int min_index = -1;
// 노드 최소값 찾기
for(int i=0; i<n; ++i){
if(!check[i]){
if(distance[i] < min){
min = distance[i];
min_index = i;
}
}
}
// 다른 노드를 거쳐서 가는 것이 더 비용이 적은지 확인한다.
check[min_index] = true;
for(int i=0; i<n; ++i){
if(!check[i] && maps[min_index][i] != Integer.MAX_VALUE){
if(distance[min_index] + maps[min_index][i] < distance[i]){
distance[i] = distance[min_index] + maps[min_index][i];
}
}
}
// 결과값 출력
for(int i=0; i<n; ++i){
if(distance[i] == 2147483647) System.out.print("∞ ");
else System.out.print(distance[i]+" ");
}
System.out.println("");
}
}
}
결과
과정을 처음부터 노드 하나마다 출력해보았다.
다익스트라 개념 게시글 내용과 같이 출력된 모습을 볼 수 있다.

우선순위 큐 방식
✔ 소스는 인접 행렬 구현에서 추가되거나 수정된 사항만 넣었다.
0. 상단에 우선순위 큐를 import 한다.
import java.util.PriorityQueue;
1. 우선순위에 넣을 노드 클래스를 선언한다.
노드까지의 가중치와 노드의 인덱스를 객체로 넣는다.
가중치를 기준으로 Comparable을 선언하여 우선순위 큐의 판단 기준을 제공한다.
class Node implements Comparable<Node>{
private int weight;
private int index;
public Node(int weight, int index) {
this.weight = weight;
this.index = index;
}
@Override
public int compareTo(Node node) {
return Integer.compare(this.weight, node.weight);
}
}
2. 우선순위 큐를 선언하고 시작 노드 및 시작 노드와 연결된 노드 정보를 큐에 넣는다.
PriorityQueue<Node> que = new PriorityQueue<>(); // 노드까지의 거리를 저장할 우선순위 큐
// 시작노드값 초기화.
que.add(new Node(v, 0));
// 연결노드 distance갱신
for(int i=0; i<n; ++i){
if(!check[i] && maps[v][i] != Integer.MAX_VALUE){
distance[i] = maps[v][i];
que.add(new Node(maps[v][i], i));
` }
}
3. 큐가 빌 때까지 큐에서 노드를 꺼내며 최소비용을 구해간다.
최소비용을 구해가는 과정은 인접 행렬 때와 같고 최소 노드를 찾는 과정만 큐에서 꺼내는 과정으로 수정되었다.
while(!que.isEmpty()){
int min = Integer.MAX_VALUE;
int min_index = -1;
// 노드 최소값 꺼내기
Node node = que.poll();
min = node.weight;
min_index = node.index;
// 다른 노드를 거쳐서 가는 것이 더 비용이 적은지 확인한다.
check[min_index] = true;
for(int i=0; i<n; ++i){
if(!check[i] && maps[min_index][i] != Integer.MAX_VALUE){
if(distance[min_index] + maps[min_index][i] < distance[i]){
distance[i] = distance[min_index] + maps[min_index][i];
que.add(new Node(distance[i], i));
}
}
}
}
전체 소스
import java.util.PriorityQueue;
public class Dijkstra {
public static void main(String[] args) {
Graph g = new Graph(6); // 노드 수 만큼 그래프 생성
// 시작, 끝, 간선 가중치 입력
g.input(0, 1, 7);
g.input(0, 2, 9);
g.input(0, 5, 14);
g.input(1, 2, 10);
g.input(1, 3, 15);
g.input(2, 3, 11);
g.input(2, 5, 2);
g.input(3, 4, 6);
g.input(4, 5, 9);
// 시작노드 기준 다익스트라 알고리즘 실행
g.dijkstra(0);
}
}
class Graph{
private int n; // 노드들의 수
private int maps[][]; // 노드들간의 가중치 저장할 변수
public Graph(int n){
this.n = n;
maps = new int[n][n];
// 인접행렬 모든 값 무한대로 초기화
for(int i=0; i<n; ++i){
for(int j=0; j<n; ++j){
maps[i][j] = Integer.MAX_VALUE;
}
}
}
class Node implements Comparable<Node>{
private int weight;
private int index;
public Node(int weight, int index) {
this.weight = weight;
this.index = index;
}
@Override
public int compareTo(Node node) {
return Integer.compare(this.weight, node.weight);
}
}
public void input(int i, int j, int w){
maps[i][j] = w;
maps[j][i] = w;
}
public void dijkstra(int v){
PriorityQueue<Node> que = new PriorityQueue<>(); // 노드까지의 거리를 저장할 우선순위 큐
int distance[] = new int[n]; // 최단 거리를 저장할 변수
boolean[] check = new boolean[n]; // 해당 노드를 방문했는지 체크할 변수
// distance값 초기화. 무한대를 int 자료형의 최대값으로 표현했다.
for(int i=0; i<n; ++i){
distance[i] = Integer.MAX_VALUE;
}
// 시작노드값 초기화.
que.add(new Node(v, 0));
distance[v] = 0;
check[v] = true;
// 결과값 출력
for(int i=0; i<n; ++i){
if(distance[i] == 2147483647) System.out.print("∞ ");
else System.out.print(distance[i]+" ");
}
System.out.println("");
// 연결노드 distance갱신
for(int i=0; i<n; ++i){
if(!check[i] && maps[v][i] != Integer.MAX_VALUE){
distance[i] = maps[v][i];
que.add(new Node(maps[v][i], i));
}
}
// 결과값 출력
for(int i=0; i<n; ++i){
if(distance[i] == 2147483647) System.out.print("∞ ");
else System.out.print(distance[i]+" ");
}
System.out.println("");
while(!que.isEmpty()){
// 원래는 모든 노드가 true될때까지 인데
// 노드가 n개 있을 때 다익스트라를 위해서 반복수는 n-1번이면 된다.
// 원하지 않으면 각각의 노드가 모두 true인지 확인하는 식으로 구현해도 된다.
int min = Integer.MAX_VALUE;
int min_index = -1;
// 노드 최소값 꺼내기
Node node = que.poll();
min = node.weight;
min_index = node.index;
// 다른 노드를 거쳐서 가는 것이 더 비용이 적은지 확인한다.
check[min_index] = true;
for(int i=0; i<n; ++i){
if(!check[i] && maps[min_index][i] != Integer.MAX_VALUE){
if(distance[min_index] + maps[min_index][i] < distance[i]){
distance[i] = distance[min_index] + maps[min_index][i];
que.add(new Node(distance[i], i));
}
}
}
// 결과값 출력
for(int i=0; i<n; ++i){
if(distance[i] == 2147483647) System.out.print("∞ ");
else System.out.print(distance[i]+" ");
}
System.out.println("");
}
}
}
결과

인접행렬때와 달리 큐가 빌 때까지 돌아서 더 출력된 모습이다.
'Java' 카테고리의 다른 글
| [JAVA] StringBuffer - 문자열 길이 조정 및 초기화 setLength (0) | 2021.04.02 |
|---|---|
| [JAVA] 문자열 및 문자를 대문자, 소문자로 변환하기 (0) | 2021.04.02 |
| [JAVA] StringBuffer - 원하는 위치 문자 제거 (0) | 2021.04.02 |
| [JAVA] char 값이 문자 인지 숫자 인지 판단하기 (0) | 2021.04.02 |
댓글