[Algorithm] 다익스트라(Dijkstra) 알고리즘 자바, 파이썬

 

개요

 

다익스트라(Dijkstra) 알고리즘은 BFS와 DP를 활용한 최단경로 탐색 알고리즘이다.

 

다이나믹 프로그래밍인 이유는 하나의 최단 거리를 구할 때 그 이전까지 구했던 최단 거리 정보를 그대로

 

사용하기 때문이다.

 

 

 

특징

 

그래프 내부 하나의 정점(노드, Vertex)에서 다른 모든 정점으로 가는 최단 경로를 알려준다.

 

그래프의 간선(Edge)마다 가중치가 존재할 때 사용한다. 이 점이 BFS를 활용한 최단 경로 구하기와 다른 점이다.

 

간선의 음의 가중치는 존재하지 않는다. 음의 가중치가 하나라도 있으면 다익스트라를 사용할 수 없다.

 

음의 가중치가 존재하지 않기 때문에 현실 세계에 사용하기 적합한 알고리즘이다. (ex. GPS, 내비게이션)

 

출발 노드, 도착 노드로 구성된

 

이차원 배열 활용 구현과 각 거리에 해당하는 우선순위 큐(힙) 활용 구현이 있다.

 

 

 

원리

 

 

 

1. 아직 방문하지 않은 정점들 중 거리가 가장 짧은 정점을 하나 선택해 방문한다.

 

2. 해당 정점에서 인접하고 아직 방문하지 않은 정점들의 거리를 갱신한다.

 

 

예를 들어

 

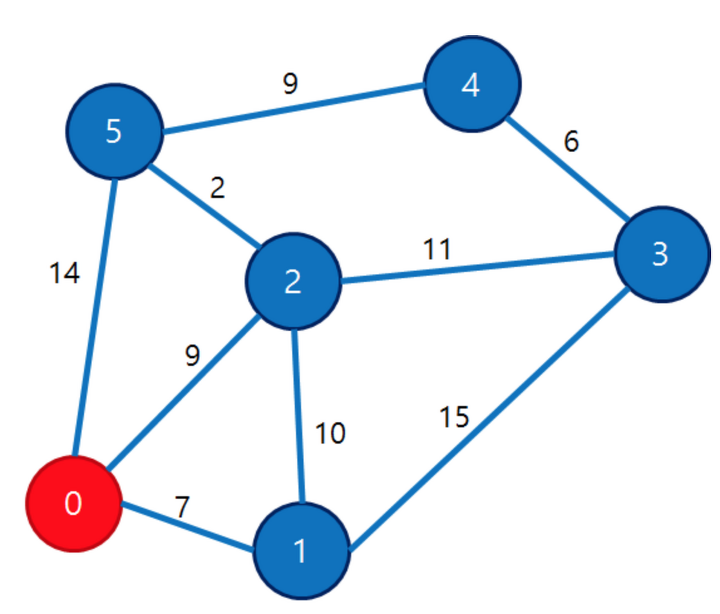
1. 시작 노드(0번 노드)를 잡고 이웃한 노드 중 거리가 가장 짧은 순으로 노드를 선택해 가중치(7, 9, 14)를

 

각각 1번, 2번, 5번 노드에 기록한다.

 

2. 1번에서 탐색한 노드(1번 노드)의 이웃한 노드 중 거리가 짧은 순으로 노드를 탐색하며

 

   처음 탐색하는 노드에는 기록된 가중치 + 간선 가중치를 기록하고

 

   재 탐색하는 노드에는 기록된 가중치 + 간선 가중치와 기록돼있는 가중치 중 작은 것을 기록한다.

 

   직접 이웃한 정점으로 가는 것보다, 이웃한 다른 정점을 거쳐서 가는 것이 더 적은 비용이 들 수도 있기 때문이다.

 

   예를 들면 위 그림에서 1번 노드에 인접한 3번 노드는 기록한 적이 없기 때문에 7 + 15 인 22를 기록한다.

 

   1번노드에 인접한 2번 노드는 9로 기록이 돼있으므로 7+10 = 17과 9 중 작은 9를 기록한다.

 

 

이 과정을 반복하여 모든 노드에 대해 탐색하면 된다.

 

탐색하는데 BFS, 가중치를 기록하고 재사용하는데 DP 원리가 쓰이게 된다.

 

 

구현

 

이차원 배열 활용 구현

 

가중치를 가중치 인접 행렬이라고 불리는 2차원 배열에 저장한다.

 

연결돼있지 않은 노드끼리는 무한대 가중치로 저장한다.

 

프로그래밍상 무한이란 값은 없으므로 구현 내 나오지 않는 최대의 값으로 지정한다.

 

 

 

 

가중치 인접 행렬은 기존의 인접 행렬과 차이점이 있다. 

 

기존의 인접 행렬에서는 간선이 없는 구간에는 행렬의 값을 0으로 했었다.

 

그러나 가중치 인접 행렬에서는 간선의 가중치 자체가 0일 수도 있기 때문에 간선이 없음을 나타낼 때 0이라는 값을

 

사용할 수가 없다.

 

위 그래프의 가중치 인접 행렬)

 

	0	1	2	3	4	5
0	0	7	9	∞	∞	14
1	7	0	10	15	∞	∞
2	9	10	0	11	∞	2
3	∞	15	11	0	6	∞
4	∞	∞	∞	6	0	9
5	14	∞	2	∞	9	0

 

 

그다음 각 노드까지의 최소 가중치를 기록할 배열을 선언한다.

 

시작 노드는 0으로 초기화한다. 시작점에서 시작점까지의 거리는 0으로 보기 때문이다.

 

나머지 노드의 가중치는 무한대로 초기화한다. 최솟값으로 비교해나갈 예정이기 때문이다.

 

 

가중치 기록 배열)

0	1	2	3	4	5
0	∞	∞	∞	∞	∞

 

 

 

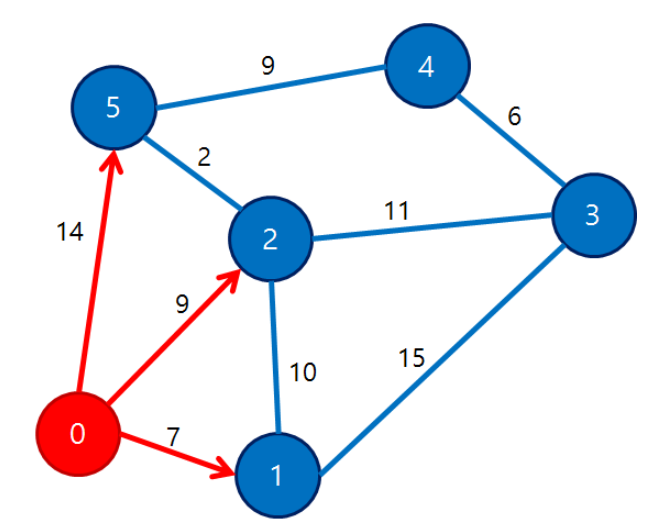
0	1	2	3	4	5
0	∞ -> 7	∞ -> 9	∞	∞	∞ -> 14

 

각 노드의 가중치 기록 배열을 dist, 가중치 인접 행렬 2차원 배열을 d라 하자.

 

시작 노드(0번)를 통해 n번 노드로 가는 거리는 dist[0] + d[0][n]이고 이게 만약 dist[n]보다 작다면 dist[n]이 갱신된다.

 

지금은 0번 노드를 제외한 모든 노드로의 dist 값이 무한대이므로 모두 갱신된다.

 

=> 시작 노드 이외 노드까지의 가중치를 무한대로 초기화하는 이유 중 하나이다.

 

그다음 인접 노드(1, 2, 5번)의 인접 노드를 탐색하며 값을 수정해나간다.

 

 

1번 노드 차례 때의 수정 예

 

 

 

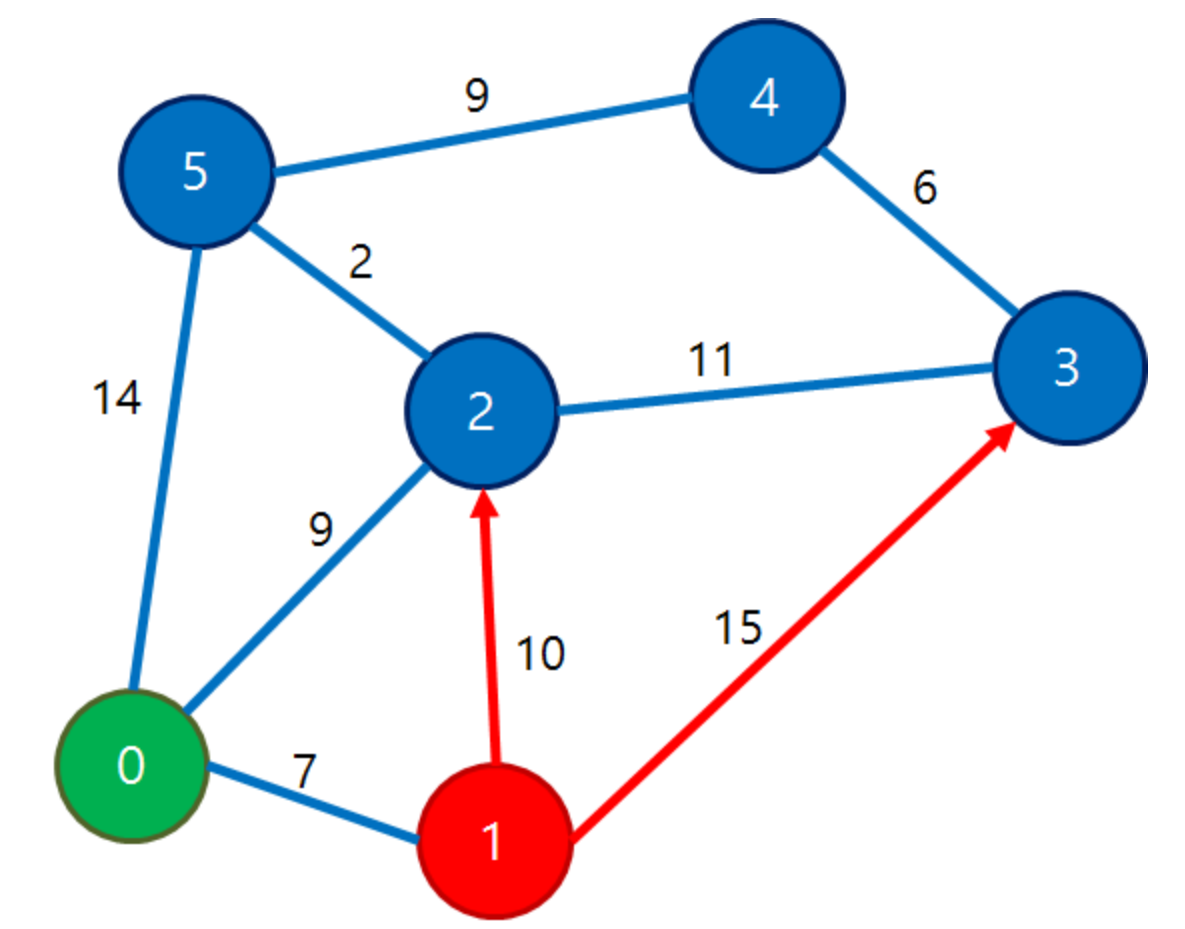
0	1	2	3	4	5
0	7	9	∞ -> 22	∞	14

 

dist[1] + d[1][3] == 7 + 15 == 22 / dist[3] == ∞ 이므로 dist[3] = 22가 된다.

 

시작 노드(0번)에서 1번 노드까지의 현재가지 기록된 최소 가중치는 7이다.

 

1번 노드 -> 3번 노드의 간선 가중치는 15이므로 기록된 가중치(0 -> 1) + 간선 가중치(1 -> 3) = 7 + 15 = 22가 된다.

 

이 값은 0 -> 3번 노드의 무한대 보다 작으므로 0 -> 3번 노드의 가중치 값을 22로 변경해준다.

 

 

dist[1] + d[1][2] == 7 + 10 = 17 / dist[2] == 9 이므로 dist[2] == 9로 남는다.

 

1번 노드 -> 2번 노드의 간선 가중치는 10 이므로 기록된 가중치(0 -> 1) + 간선 가중치(1 -> 2) = 7 + 10 = 17이 된다.

 

이 값은 0 -> 2번 노드에 기록된 가중치 9보다 크므로 변경하지 않고 넘어간다.

 

 

 

2번 노드 차례 때의 수정 예

 

 

 

0	1	2	3	4	5
0	7	9	22 -> 20	∞	14 -> 11

 

dist[2] + d[2][3] == 9 + 11 == 20 / dist[3] == 22 이므로 dist[3] = 20이 된다.

 

시작 노드(0번)에서 2번 노드까지의 현재가지 기록된 최소 가중치는 9이다.

 

2번 노드 -> 3번 노드의 간선 가중치는 11이므로 기록된 가중치(0 -> 2) + 간선 가중치(2 -> 5) = 9 + 11 = 20이 된다.

 

이 값은 0 -> 3번 노드의 22보다 작으므로 0 -> 3번 노드의 가중치 값을 20으로 변경해준다.

 

 

dist[2] + d[2][5] == 9 + 2 == 11 / dist[5] == 14 이므로 dist[5] = 11이 된다.

 

시작 노드(0번)에서 2번 노드까지의 현재가지 기록된 최소 가중치는 9이다.

 

2번 노드 -> 5번 노드의 간선 가중치는 2이므로 기록된 가중치(0 -> 2) + 간선 가중치(2 -> 5) = 9 + 2 = 11이 된다.

 

이 값은 0 -> 5번 노드의 14보다 작으므로 0 -> 5번 노드의 가중치 값을 11로 변경해준다.

 

 

5번노드 차례 때의 수정 예

 

 

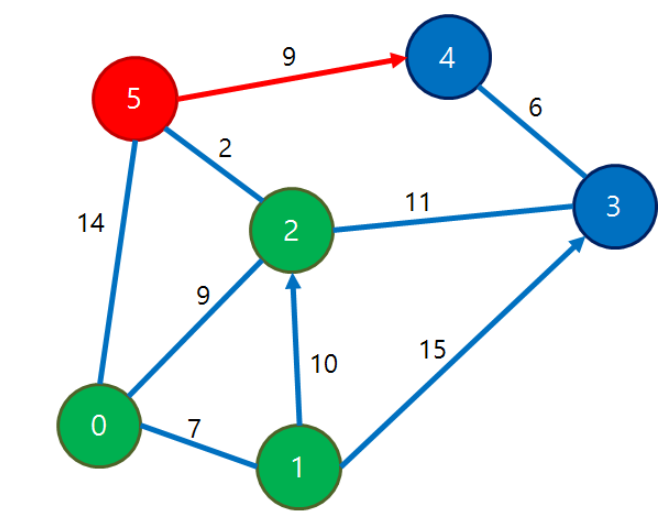
0	1	2	3	4	5
0	7	9	20	∞ -> 20	11

 

dist[5] + d[5][4] == 11 + 9 == 20 / dist[4] == ∞ 이므로 dist[4] = 20이 된다.

 

시작 노드(0번)에서 5번 노드까지의 현재가지 기록된 최소 가중치는 11이다.

 

5번 노드 -> 4번 노드의 간선 가중치는 9이므로 기록된 가중치(0 -> 5) + 간선 가중치(5 -> 4) = 11 + 9 = 20이 된다.

 

이 값은 0 -> 54번 노드의 무한대보다 작으므로 0 -> 4번 노드의 가중치 값을 20으로 변경해준다.

 

 

 

3번 노드 차례 때의 수정 예

 

0	1	2	3	4	5
0	7	9	20	20	11

 

dist[3] + d[3][4] == 20 + 6 = 26 / dist[4] == 20 이므로 dist[4] == 20으로 남는다.

 

3번 노드 -> 4번 노드의 간선 가중치는 6이므로 기록된 가중치(0 -> 3) + 간선 가중치(3 -> 4) = 20 + 6 = 26이 된다.

 

이 값은 0 -> 4번 노드에 기록된 가중치 20보다 크므로 변경하지 않고 넘어간다.

 

 

 

 

마지막 4번 노드는 이웃한 모든 노드가 탐색을 완료한 상태기 때문에 더 이상 탐색하지 않는다.

 

 

 

 

모든 노드를 탐색한 후 나온 가중치 테이블이 시작 노드(0번 노드)로 부터의 최단거리 테이블이다.

 

0	1	2	3	4	5
0	7	9	20	20	11

 

예)

시작 노드(0번 노드)부터 1번 노드까지 최단 거리 : 7

시작 노드(0번 노드)부터 2번 노드까지 최단 거리 : 9

시작 노드(0번 노드)부터 3번 노드까지 최단 거리 : 20

시작 노드(0번 노드)부터 4번 노드까지 최단 거리 : 20

시작 노드(0번 노드)부터 5번 노드까지 최단 거리 : 11

 

 

이차원 배열 활용 구현의 시간 복잡도

 

아직 방문하지 않은 정점들 중에서 dist 값이 제일 작은 노드를 찾아 방문하는 부분 => O(V)

 

모든 노드 탐색 => O(V)

 

로  O(V^2)의 시간 복잡도가 발생한다.

 

 

dist 값이 제일 작은 노드를 찾는 부분을 우선순위 큐를 이용하면 O( log V )로 줄일 수 있다.

 

따라서 우선순위 큐를 이용하면 O( V log V )로 시간 단축이 가능하다.

 

 

 

우선순위 큐 활용 구현

 

최소 힙을 하나 마련한다.

 

어떤 노드 u를 방문해서 인접한 노드 v의 거리를 갱신할 때마다 최소 힙에 (dist[v], v) 쌍을 넣는다.

 

힙의 pair는 첫 번째 인자의 대소 비교를 먼저 하므로, dist 값이 작으면 작을수록 우선순위 큐에서 먼저 나오게 된다.

 

그 두 번째 인자인 정점 번호를 사용하면 된다.

 

 

주의사항

 

1. v를 방문하기 전에 값이 여러 번 갱신될 수도 있고 서로 다른 (dist[v], v) 값들이 우선순위 큐 안에 존재할 수 있다.

 

이 때는 제일 작은 d 값 하나만 뽑아서 쓰면 되고 우선순위 큐가 이걸 자동으로 해결해 준다.

 

2. 1번 사항으로 인해 뽑히지 못하고 우선순위 큐에 남아있는 v 정점에 관한 쌍의 처리 문제

 

큐에서 나온 노드가 이미 방문한 노드라면 무시하는 코드를 구현한다.

 

 

 

소스코드

 

자바

 

[JAVA] 다익스트라(dijkstra) 자바로 구현하기

[JAVA] 다익스트라(dijkstra) 자바로 구현하기

 

곧 파이썬 카테고리에 업데이트 예정이다.